`" Linear stability \ of plane Poiseuille flow \ over a steady Stokes layer \ \small [Documento completo \href{./tesi-sovardi.pdf}{qui} ]

Linear stability
of plane Poiseuille flow
over a steady Stokes layer
[Documento completo qui ]

Carlo Sovardi

The linear stability of plane Poiseuille flow subject to spanwise velocity forcing applied at the wall is studied. The forcing is stationary and sinusoidally distributed along the streamwise direction. The long-term aim of the study is to explore a possible relationship between the modification induced by the wall forcing to the stability characteristic of the unforced Poiseuille flow and the significant capabilities demonstrated by the same forcing in reducing turbulent friction drag.
This work presents the statement of the mathematical problem, which is quite more complex than the classic Orr-Sommerfeld-Squire approach. Complexities arise owing to the form of the forcing velocity at the wall, which makes the streamwise direction non-homogeneous. We aim at exploring the main physical parameters that influence the stability of a plane Poiseuille flow subject to the varying boundary condition comparing it with the reference unforced problem. We present some preliminary results, although not yet conclusive, which describe the main effects of wall forcing on modal and nonmodal stability of the flow at different flow conditions.
The linear stability of plane Poiseuille flow modified by a wall velocity forcing in the form of streamwise stationary waves of spanwise velocity has been analyzed. The forcing applied at the wall has the form:
w = A ( κx )
and the various quantities are made dimensionless with the centerline velocity of the laminar Poiseuille flow and half the gap width.
Both modal and non-modal stability characteristics have been studied by looking respectively to the real part of the least stable eigenvalue and to the maximum of the transient energy growth function, in comparative form with respect to the standard Poiseuille flow.
The mathematical formulation and its implementation of linearized wall-normal velocity and vorticity equations are not straightforward in this case, since the wall forcing introduces an inhomogeneity in streamwise direction. The simple transform in Fourier space to decouple wavenumbers transforming the problem to a parametric one-dimensional eigenvalue study does not work in this case. Hence we have to consider a sufficient large set of wavenumbers in streamwise direction to describe correctly the spatial non-homogeneity of the present problem. The problem is thus global in the streamwise direction.
The linearized equations have been discretized using Chebyshev polynomials and integrated with a Gaussian quadrature over Gauss-Lobatto nodes. Reliability of results has been verified against a DNS code.
The results of the modal stability analysis show that:
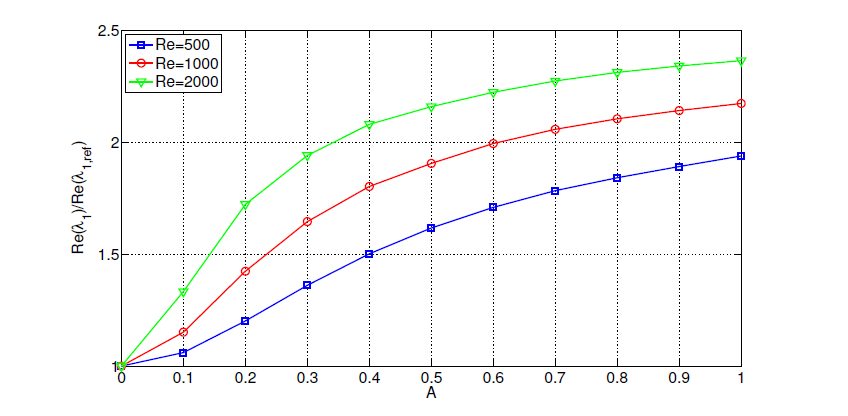
modal-stability.png
Figure 1: Maximum relative reduction of the least-stable eigenvalue, as a function of the forcing intensity A, for any considered value of the Reynolds number.
The results of the non-modal stability analysis show that:
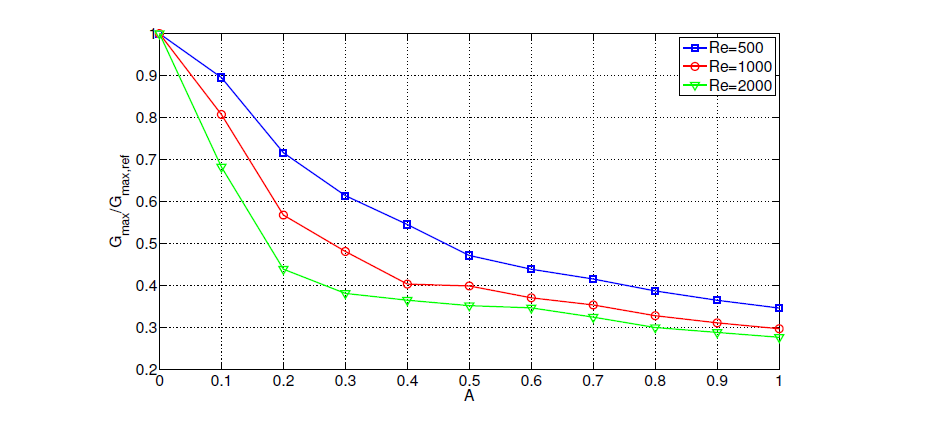
non-modal-stability.png
Figure 2: Maximum relative reduction of the transient growth function, as a function of the forcing intensity A, for any considered value of the Reynolds number.
In conclusion, the steady Stokes layer offers important improvements on both modal and non-modal stability properties of the plane Poiseuille flow. These improvements reach their maximum values imposing a wall forcing with κ ≈ 1 and A = 1.


File translated from TEX by TTH, version 4.03.
On 17 Sep 2012, 17:37.